The geometrical characterization of complex spatial structures is generally a difficult problem. One direction consits in firstly defining a stochastic geometrical model which can be fitted to the real data. For example, boolean models (union of random elementary geometrical sets) can be used to simulate complex structures geometrically similar to the data. Then, the geometrical characterization of such modeled spatial structures becomes easier.
Stochastic geometrical image analaysis is here applied to crystallization processes. The objective is to estimate the granulometry of the crystals. Boolean models are then fitted to the data according to some measurements of integral geometry (Minkowski functionals). In this way, geometrical characteristics of the individual crystals can be statistically estimated, despite the fact that crystals are superimposed.

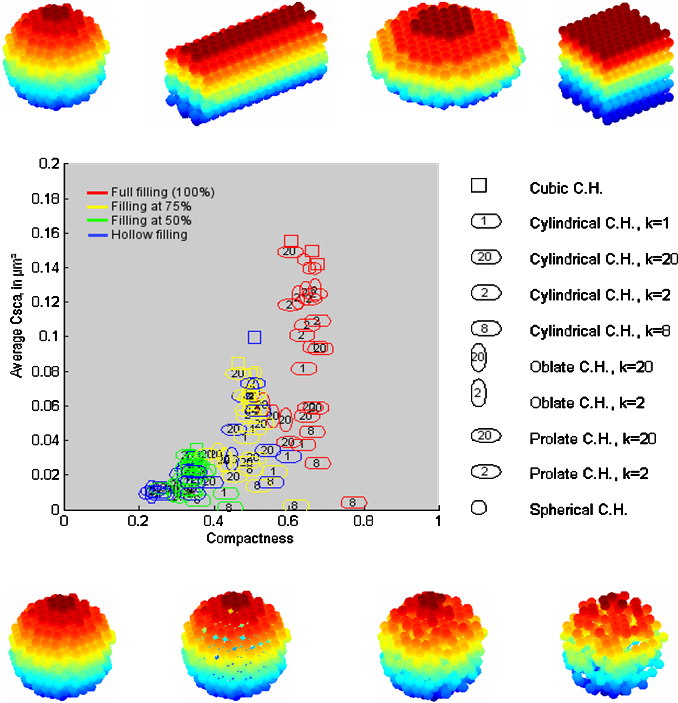The main objective of image analysis is to provide a quantitative characterization of the different image structures. In the literature, numerous geometrical and morphometrical characterizations have been introduced, especially for pattern recognition.
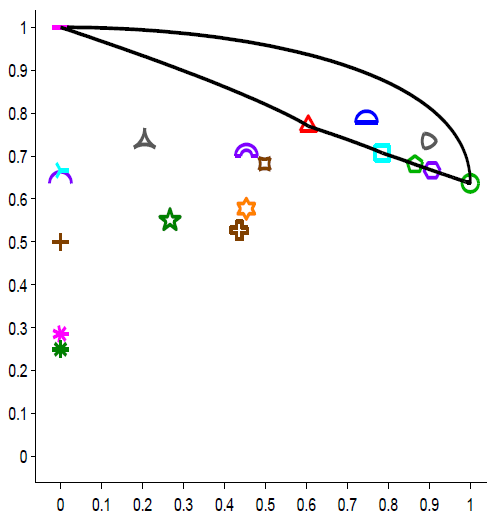
In this way, shape diagrams are an original concept where a single shape (i.e., mathematically a connected compact set) is represented as a point in the 2D plane unit square. They can be viewed as tools for shape discrimination. A successful application example has been reported in quantitative projective stereology allowing the 3D geometrical characterization of convex objects by means of 2D measurements (using shape diagrams) on a few projected figures. Shape diagrams have been also combined with the GANIP approach for the characterization of gray tone images (without any segmentation).
Nevertheless, most of the geometrical/morphometrical descriptors are generally based on strong hypotheses (simply connected objects, regular contours. . . ) and then provide unsuitable descriptors for complex objects (e.g. aggregates). The characterization of such objects need the use of spatial descriptors of point/pattern processes.

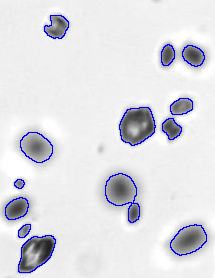
The General Adaptive Neighborhood Image Processing (GANIP) is a mathematical framework for adaptive processing and analysis of gray-tone images. An intensity image is represented with a set of local neighborhoods defined for each pixel of the image to be studied. Those so-called General Adaptive Neighborhoods (GANs) are simultaneously adaptive with the spatial structures, the analyzing scales and the physical settings of the image to be addressed and/or the human visual system. The GANs are then used as adaptive operational windows for local gray-tone image transformations (morphological filters, rank/order filters...) and for local image analysis (local descriptors, distance maps...).
Successful application examples have been reported in several image processing areas, e.g., image enhancement, image filtering, image restoration, image focus measurement, edge detection and image segmentation.

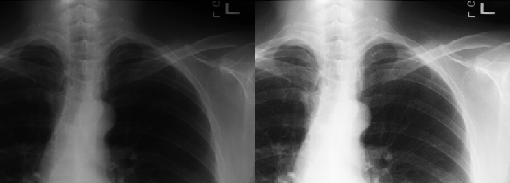The Logarithmic Image Processing (LIP) approach is a mathematical framework, introduced in the middle of the 1980's, based on abstract linear mathematics which provides a set of specific algebraic and functional operations that can be applied to the processing of intensity images valued in a bounded range. The LIP approach has been proved to be physically justified in the setting of transmitted and reflected light imaging, and to be consistent with several laws and characteristics of the human brightness perception.
Successful application examples have been reported in several image processing areas, e.g., image enhancement, image filtering, image restoration, three-dimensional image reconstruction, edge detection and image segmentation.