Nous n'abordons ici que la régression linéaire multivariables. Pour plus de détails sur la régression linéaire (monovariable: y=ax+b), qui est un cas particulier, voir le chapitre "étalonnage" du document "Incertitude de mesure & Etalonnage"
Les relations entre les X et les Y sont linéaires et les ap forment une matrice A:
Y=XA + E

(On pourra, si nécessaire, consulter les rappels d'algèbre linéaire).On peut montrer facilement que l'équation (1) du paragraphe précédent est équivalente à un système de c équations à n inconnues ak dont la solution, au sens "moindres carrés", est:
Remarque: La convention chimiométrique pour l'écriture des matrices, sera utilisée: Chaque ligne représentera un échantillon (ou expérience) et chaque colonne, une variable.
Représentations
graphiques:
Ces représentations peuvent permettre de mieux comprendre les
problemes:

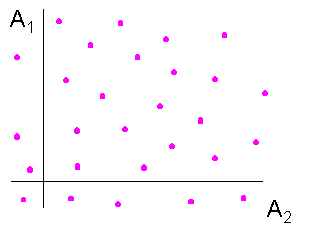
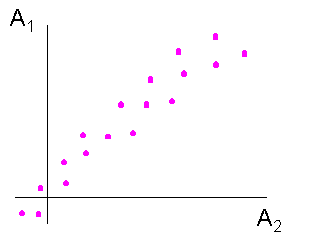
A1 et A2 indépendantes A1 et A2 non indépendantes
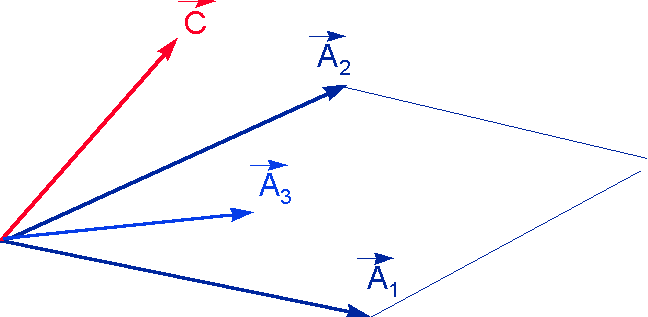

On remarque que faire une régression de Y sur X consiste à projeter Y sur le plan des X. A est alors la matrice de projection dans le plan des X.
En effet, on cherche à écrire Y sous forme de combinaison linéaire de X1 et X2: la chose est impossible puisque Y n'est pas dans le plan (X1,X2), mais on va s'en approcher en minimisant le vecteur E, différence entre Y et la combinaison linéaire.
L'étalonnage sera d'autant meilleure que Y sera près du plan des X. E représente les variations de Y non corrélées avec celles de X et donc pas expliquées par le modèle.
Quelques éléments supplémentaires:
Exemple de la loi de Beer Lambert
Reprenons l'exemple de la colorimétrie et de la loi de Beer Lambert. On appelle:
Méthodes de moindres carrés dites "simples":aik = absorbance de l'échantillon i à la longueur d'onde lk
cij = concentration de l'échantillon i en composé jLa loi de Beer Lambert s'écrit, sous forme matricielle:
La loi de Beer Lambert servira de support pour la suite de l'exposé, mais les applications de l'analyse multivariables ne se limitent pas à la colorimétrie et sont innombrables.
* Première méthode: CLS (Classic Least Squares) ou Kmatrice:On recherche une estimation de la matrice K des coefficients de Beer Lambert
On va minimiser E, c'est à dire les erreurs sur les absorbances,
on va donc régresser A sur C.
On obtient alors la matrice K:
En phase prédiction, on a: A=CK, mais c'est la matrice C que
l'on veut déterminer.
Or K est généralement non carrée donc non inversible.
On peut quand même écrire:
M est alors la matrice de prédiction.
On est amené à effectuer 2 inversions de matrices carrées
de faible dimension (dimension = nombre de composés):
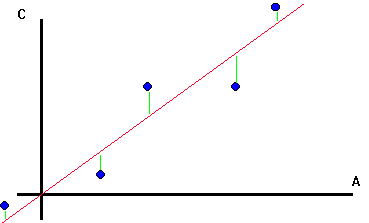
Exemple graphique avec 3 échantillons, 2 longueurs d'onde et 1 composé:
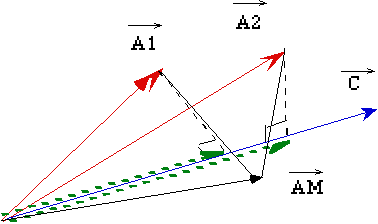
On déduit des projections de A1 et A2 sur C les coefficients de Beer Lambert k1 et k2. En fait, si le nombre de longueurs d'onde est supérieur au nombre de composés (ce qui est généralement le cas), l'information est redondante: Le prédicteur M est en fait une "moyenne" des différents opérateurs projection pour les différents Ak, ce qui augmente théoriquement la précision du résultat.
C'est en fait le principe de la régression linéaire
où l'on dispose généralement d'un nombre de points
supérieur au nombre strictement necessaire, mais ceci permet de
créer un meileur modèle.
Application: Détection des nitrates dans l'eau potable:
Avantages de la méthode Kmatrice:
Représentation graphique: 3 échantillons, 2 longueurs et 1 composant.Avantage majeur de cette méthode:
On projette C sur le plan (A1 A2). La matrice de prédiction P est la matrice de cette projection. E représente la partie de la concentration dont il n'est pas tenu compte dans le calibrage (variations non corrélées avec les variations d'absorbance).
Cette méthode résout donc le
problème des impuretés, mais celles-ci doivent être
présentes de façon significative dans les échantillons
de calibrage.
De façon plus générale,
il résoud le problême des variations dues à des causes
externes, celles-ci n'ont pas à être quantifiées pendant
la phase de calibrage, mais doivent, répétons-le, être
présentes de façon "significative".
Application: mesure nitrates dans l'eau avec un interférent: Les acides humiquesInconvénients:
De plus, si des absorbances de longueurs d'onde trop voisines sont "presque" colinéaires (physiquement non inversible), A'A, même si elle est mathématiquement inversible, aura un déterminant faible. La matrice P aura alors de forts coefficients (en valeur absolue) et il y aura des problèmes d'instabilité pendant la prédiction.
Enfin, retrouve ici le probleme de surmodélisation,
commun aux 2 méthodes CLS et ILS, notamment lorsque le nombre d'échantillons
est faible.
La surmodélisation apparait lorsque le modèle est trop précis, on tend alors à modéliser les "particularités des échantillons d'étalonnage, alors que seule l'information "généralisable" nous interesse.
Une premiere solution à ce probleme consiste à avoir un très grand nombre d'échantillons, mais cela est couteux.
Une autre solution consiste en l'utilisation d'un algorithme permettant de n'utiliser autant que possible que la partie utile des informations de calibrage (c'est à dire, dans le cas de Beer Lambert, les variations d'absorbances et de concentration réellement corrélées entre elles) qui au départ sont redondantes.
Une autre façon de voir les choses est de constater que, par les méthodes classiques, on va modéliser le plus d’information possible, qu’elle soit représentative de la réalité physique ou qu’elle soit juste du bruit de mesure. On risque alors de faire de la sur-modélisation: le modèle est trop complexe et ne s’appliquera correctement qu’aux échantillons ayant servi à le créer.
De plus, même si le modèle est correct physiquement,
on peut constater, lors de la prédiction, que plus un modèle
est complexe, plus les erreurs (relatives) de mesure sur les
variables X seront amplifiées lors du calcul des variables
Y, d’où les dangers de la sur-modélisation .
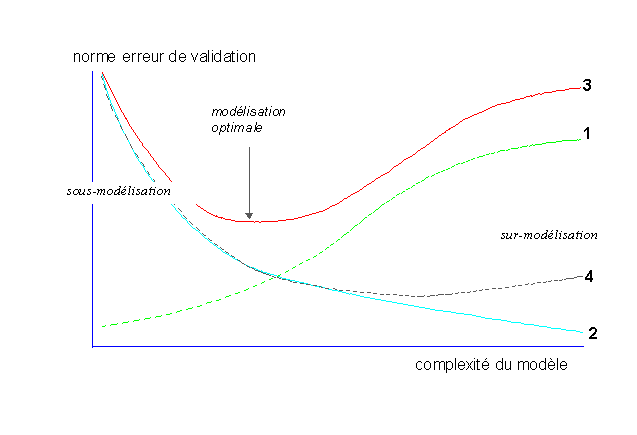
Toutefois, les effets de la sur-modélisation, prépondérant
si les échantillons de calibrage sont peu nombreux, tendent à
diminuer si l’on en dispose de beaucoup, ce qui n’est pas toujours évident.
A l’opposé, si le modèle est trop simple, il y aura peu de propagation de l’erreur de mesure, mais il sera peu performant en prédiction car il ne reflétera pas suffisamment la réalité physique, on parle alors de sous-modélisation.
Ainsi, cette modélisation aboutit à un compromis entre un modèle simple et robuste (tolérant vis à vis des erreurs de mesure) mais peu précis et un modèle complexe, précis mais fragile.
Il apparaît donc intéressant de pouvoir choisir la complexité
du modèle en fonction du phénomène étudié
et des qualités métrologiques des mesures.
Remarque: Ces considérations sur la sur ou sous-modélisation, bien que comprises dans le chapitre " linéaire ", on un caractère plus général, comme on pourra le constater avec les réseaux neuronaux.L'analyse de facteurs:
L'analyse de facteurs consiste à faire un changement de variable au niveau des Xvariables. On prend alors, comme nouvelles Xvariables, des combinaisons linéaires des anciennes Xvariables, en nombre réduit afin de concentrer l'information utile.
Il y a, initialement, n Xvariables, généralement plus ou moins corrélées entre elles. Le but est de trouver de nouvelles variables indépendantes, combinaisons linéaires des anciennes. Ces variables sont appelées facteurs ou variables latentes et leur valeur pour un échantillon donné, score.
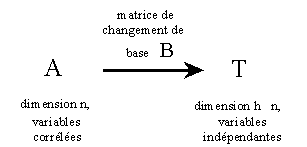
Si h=n, il n'y a pas de réduction de données, le problème
est équivalent au précédent et la méthode a
peu d'intérêt.
Il y a plusieurs méthodes pour déterminer la matrice
de changement de base B ("Loadings vecteurs") qui seront explicitées
plus loin.
Pendant la prédiction, le changement de base permettant de connaître
les scores T se fait comme suit:
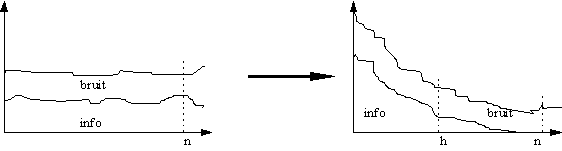
L'intérêt de cette compression de données est que, faute de pouvoir éliminer le bruit de mesure, on s'arrange pour que l'information utile, qui pouvait être initialement répartie sur tout le spectre, se retrouve dans les premiers facteurs qui seront seuls utilisés, donc dans les scores. Or le bruit reste également réparti pour tous les facteurs: l'information "abandonnée" n'est donc pratiquement que du bruit, et on a donc globalement une réduction de celui-ci.
On peut ensuite calculer les concentrations par régression
de T à partir d'une matrice de prédiction V déterminée,
pendant le calibrage, par ILS à partir des scores:
On élimine ainsi les inconvénients des 2 précédentes méthodes:
Dans les 2 cas, on réduit le risque d'"overfitting" (modélisation
du bruit) en réduisant le nombre de variables.
Il existe principalement 2 méthodes d'analyse des facteurs:
* PCR (Principal Component Régression)Cette méthode utilise la matrice des covariances des absorbances centrées, A'A. Elle part du principe que pour choisir une nouvelle base de variables indépendantes, il suffit, par définition, que les covariances de ces variables entre elles soient nulles. La matrice de changement de base est donc la matrice qui va rendre la matrice de covariance diagonale. Elle est donc construite à partir des vecteurs propres de A'A. Les valeurs propres représentent alors la variance des scores, et donc leur contribution à la modélisation: Pour effectuer la réduction de données, il suffit alors de ne conserver que les h scores correspondant aux plus fortes valeurs propres.
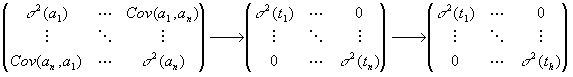
h £ n
Cette méthode est très efficace, mais elle ne tient pas compte dans la première phase de calibrage, (choix de la nouvelle base) des informations concentration, qui ne sont utilisées que dans la phase de régression des concentrations sur les scores.
Il peut pourtant arriver que des effets importants sur les absorbances
ne soient absolument pas corrélés avec les concentrations.
On lui préfère donc souvent une méthode plus récente
et plus complexe:
* PLS (Partial Least Squares):Cette méthode, plus récente (1980), consiste à construire ensembles les matrices de changement de base W ("Loadings Vectors") et de prédiction V en utilisant conjointement les absorbances et les concentrations.
Modélisation PLS (1 seule Yvariable)
Cette méthode de prédiction (ainsi que PCR) a l'avantage de fournir, en plus de la concentration, les résidus d'absorbances (information absorbance restant à la fin de la prédiction, donc non utilisée) qui doivent théoriquement être du même ordre de grandeur que ceux obtenus lors du calibrage. L'examen du rapport (résidu de prédiction / résidu de calibrage) pour chaque longueur d'onde peut alors permettre de détecter des anomalies, notamment la présence d'impuretés non présentes lors du calibrage. On peut alors supposer que le calcul de prédiction risque d'être erroné.
Exemple: Détection des nitrates, présence de Cr3 uniquement pendant la prédiction:En fait, pour chaque calcul de prédiction, on préfère souvent calculer un terme "d'erreur probable" appelé déviation (cf logiciel "Unscrambler"):
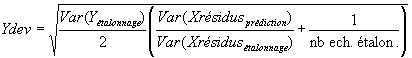
(Ce terme est à multiplier par la norme des
concentration d'étalonnage si celles-ci ont été normées).
Ce terme a, dans la plupart des cas, la même ordre de grandeur
que l'écart type de l'erreur de prédiction.
* Problème commun aux 2 méthodes: Le choix du nombre de facteurs:Nous avons vu qu'il était nécessaire d'arrêter l'étalonnage pour un nombre de facteurs donnant des résultats de prédiction optimaux. C'est à dire, dans le cas de PLS, quand les résidus d'absorbance deviennent du même ordre de grandeur que le bruit de mesure, l'information utile ayant été extraite.
Il faut donc, pour chaque nouveau facteur, faire des tests afin de minimiser la variance des erreurs de prédiction. Ces tests ne doivent en aucun cas être faits avec les échantillons d'étalonnage sinon on trouverait un nombre de facteurs optimal égal au nombre maximum de facteurs: On arriverait alors à retrouver les concentrations d'étalonnage avec précision, le bruit de mesure modélisé étant reconstitué. Mais avec d'autres échantillons, les performance seraient mauvaises.
Il est donc nécessaire:

Remarque: nombre de facteurs =