Cas où on peut par des transformations se ramener à des fonctions linéaires:
Dans certains cas , une modélisation avec une méthode linéaire est directement possible, sinon, il est souvent possible de faire une...

Linéarisation:

Il suffit alors de transformer les variables pour l'étalonnage comme pour la prédiction:

Cas particulier classique: la régression polynomiale: une seule variable x remplacée par n variables x₁...x_n:

Ainsi, si la fonction est peu non-linéaire, on va pouvoir la modéliser à l'aide d'un polynome: il suffira d'ajouter des variables carré, cube etc..., voire, dans le cas multivariable, des produits croisés. Mais le nombre de variables va rapidement devenir important.

---

 

* Méthode de Newton:

Pour tout q, 1 £ q £ p: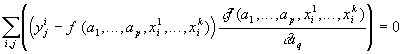 
qui peut se ramener à:

Ce système peut se résoudre itérativement par la méthode de Newton, qui consiste, en résumé à trouver une estimation de la solution a10...ap0, puis à linéariser aux environs de ce point, et enfin à résoudre le système d'équations linéaires. Il faut ensuite recommencer avec les solutions jusqu'à la convergence souhaitée.

Soient (a10...ap0) une estimation de la solution. On peut alors supposer que

Pour tout q, 1 £ q £ p: 
soit, en faisant un développement limité du premier ordre autour de ce point:

Pour tout q, 1 £ q £ p: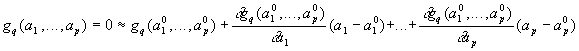 
qui est un système de p équations linéaires de solution (a11...ap1). Il suffit alors de recommencer en linéarisant de nouveau autour de ce point jusqu'à la convergence souhaitée.
C'est une méthode à convergence rapide et qui ne nécessite qu'un point de départ. Mais elle est analytiquement très lourde (il faut connaître analytiquement les dérivées des fonctions gq et donc les dérivées secondes des fonctions fj!) et la résolution des systèmes linéaire oblige à inverser une matrice de dimension p: si cette matrice est singulière ou presque, le risque de blocage ou de divergence est grand.

Les 2 méthodes suivantes sont des méthodes dites d'optimisation. Ces méthodes consistent à optimiser une grandeur vers un état extrémal (minimal en ce qui nous concerne) en faisant évoluer ses variables.

La grandeur qui nous intéresse est:

Nous développerons le cas de 2 paramètres a1 et a2, mais les méthodes sont généralisables mais plus complexes pour des dimensions supérieures.

Ces méthodes sont donc des méthodes itératives partant d'un ou plusieurs points initiaux et se dirigeant plus ou moins lentement mais sûrement vers la solution:

---

* Steepest gradient:

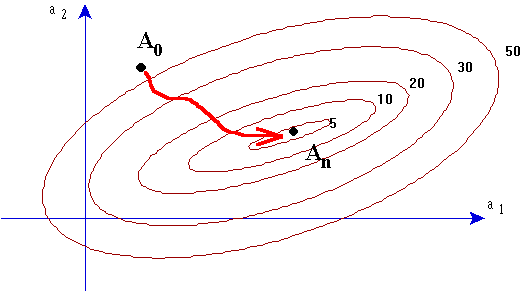
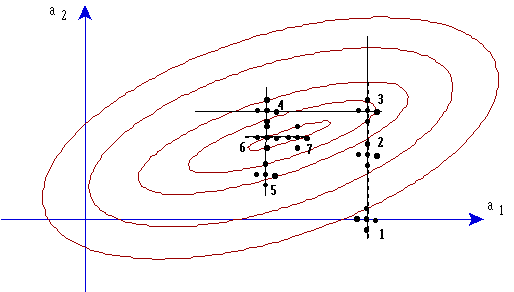
A partir d'un point initial, calculer les valeurs correspondant à 4 autres points répartis autour de ce point, et alignés 2 à 2 avec lui:

Choisir comme direction celle du point donnant la plus faible valeur et placer le point suivant dans cette direction.à une distance dq. Si la nouvelle direction est opposée à la précédente (point 6), prendre un point situé entre le dernier et l'avant dernier. On peut aussi, si la nouvelle direction est la même, doubler dq. Il existe en fait de nombreuses variantes, plus ou moins élaborées pour placer le point suivant.

* Méthode du simplex:

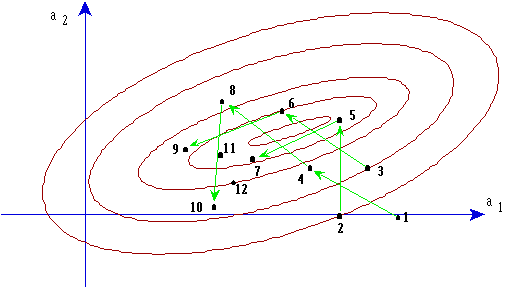
Les règles pour placer le point suivant sont les suivantes:
 

• Un nouveau triangle est crée en éliminant le point du triangle précédent donnant la réponse (= somme des moindres carrés) la plus forte et en prenant comme nouveau point son symétrique par rapport aux 2 autres points (points 4,5,6,7 et 8).
• Si le point obtenu donne aussi la plus forte réponse, on utilise alors, pour faire la symétrie, le point donnant la deuxième plus forte réponse (point 9).
• Si un point est "sélectionné" plus de 3 fois (point 7), il est le point donnant la valeur la plus faible que l'on puisse obtenir avec la taille de triangle choisie.
• On peut alors continuer à partir de ce point avec des triangles plus petits.